Interphone Immeuble Collectif IP
Comment fonctionne un interphone d’immeuble ?
Chaque complexe résidentiel est une installation fermée autonome destinée uniquement aux résidents et à leurs invités. Les étrangers ne devraient pas être ici. Par conséquent, toute une gamme de mesures est prévue pour contrôler les visiteurs, y compris les interphones d’accès, CCTV (système de vidéosurveillance) et ACS (système de contrôle d’accès), qui fonctionnent en conjonction les uns avec les autres.
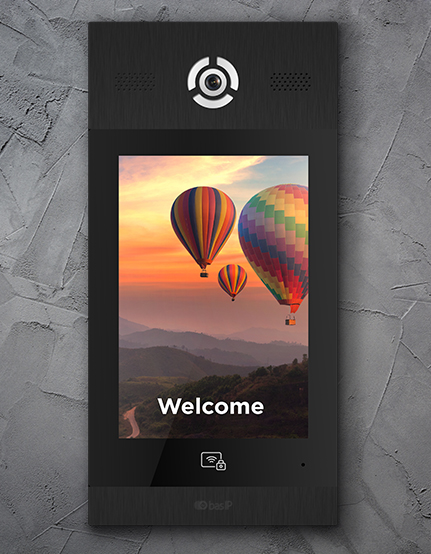
Platine interphone immeuble – RESTERA DANS LES MÉMOIRES POUR TOUJOURS
La première chose qui accueille un invité à l’entrée du complexe résidentiel ou de l’entrée est le platine de porte de l’interphone collectif. C’est le point où la communication commence. Les panneaux extérieurs BAS-IP sont disponibles dans une variété de couleurs et de designs et peuvent être équipés de nombreuses caractéristiques uniques, qui sont décrites ci-dessous.
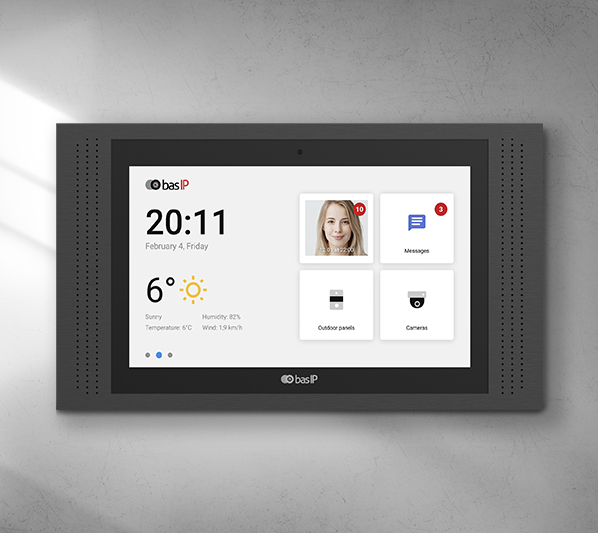
Interface pratique, intuitive et accessible
Notre département de conception UX effectue de nombreux tests pour s’assurer que notre interface d’interphone multi-unités est compréhensible pour tout résident ou invité entrant dans le complexe résidentiel. En choisissant notre système d’interphone, vous ne recevrez que des commentaires positifs à son sujet.
Colonne Interphone Copropriete Exclusif

Possibilités maximales
-
 Reconnaissance faciale automatique
Reconnaissance faciale automatique
-
 Appel du concierge
Appel du concierge
-
 Écran tactile IPS 10″
Écran tactile IPS 10″
-
 Appeler l’ascenseur à l’étage
Appeler l’ascenseur à l’étage
-
 Assistance UKEY
Assistance UKEY
-
 Configuration flexible du système
Configuration flexible du système
-
 Contacter le carnet
Contacter le carnet
-
 Température de travail -40 – +65 °С
Température de travail -40 – +65 °С
PRIX DE CONCEPTION
Fonctionnement interphone collectif
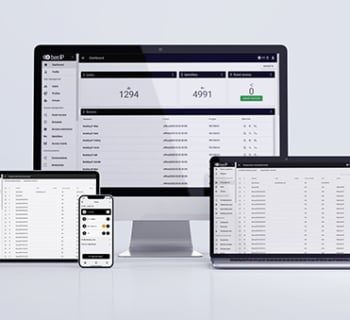
LOGICIEL DE GESTION DU SYSTÈME D’INTERPHONE BAS-IP LINK
Le logiciel Link offre un panneau de contrôle d’accès centralisé qui vous permet de vous connecter à n’importe quel interphone collectif BAS-IP installé dans un immeuble. Il vous permet de gérer de manière flexible toutes les fonctions du système d’interphonie depuis n’importe où dans le monde. Vous pouvez utiliser Link sur n’importe quel appareil : ordinateur, tablette ou appareil mobile iOS/Android.

CONTINUITÉ DE FONCTIONNEMENT DU SYSTÈME D’INTERPHONE
Récemment, un interphone a gagné en popularité dans un immeuble d’habitation, dans lequel une application mobile est utilisée à la place d’un interphone physique. Mais que se passe-t-il si un smartphone ou une connexion Internet n’est pas disponible ? Dans notre interphone IP multi-appartements, l’appel est dupliqué vers un appareil physique situé dans l’appartement.

BOÎTIERS ET INTERFACES PERSONNALISÉS
En plus des solutions standardisées adaptées à la plupart des tâches, BAS-IP peut proposer le développement d’interfaces et de boîtiers individuels uniques pour un complexe résidentiel spécifique. Une excellente solution qui soulignera le caractère unique de tout projet.

Publicité sur l’intercom porte d’entrée
Les platines de rue d’appel des complexes résidentiels peuvent afficher des messages informatifs ou publicitaires sur leurs écrans en mode veille ou lorsqu’un mouvement est détecté devant la platine.
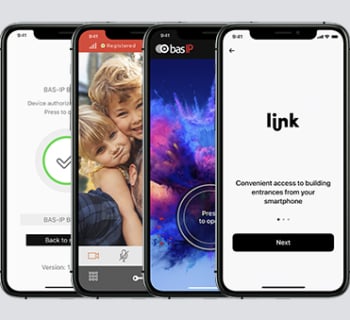
PRE-INSTALLATION DE L’APPLICATION MOBILE DU CLIENT
La plupart des complexes résidentiels modernes ou des colonies de chalets développent leur propre application. Selon nos statistiques, plus de la moitié des entreprises souhaitent l’intégrer dans le système d’interphonie. BAS-IP peut le faire dès le stade de la production. Votre application ne sera pas désinstallable, elle sera fixée sur l’écran principal du moniteur interphone.

INTÉGRATION AU SYSTÈME DE SURVEILLANCE VIDÉO
La vidéo des panneaux extérieurs installés à l’entrée peut être transférée au DVR pour un enregistrement et une surveillance continus. De plus, les caméras IP peuvent être visualisées sur des moniteurs BAS-IP.

API OUVERTE
L’équipe R&D de BAS-IP a implémenté une API JSON pour prendre en charge les grandes installations où le système d’interphonie fait partie d’une grande suite logicielle.

CONNEXION DE LA BOUCLE D’INDUCTION
L’installation d’une boucle d’induction assure une transmission de haute qualité du signal audio du panneau d’appel vers les implants cochléaires et les aides auditives pour sourds.
Améliorer la qualité de vie des résidents et de leurs invités
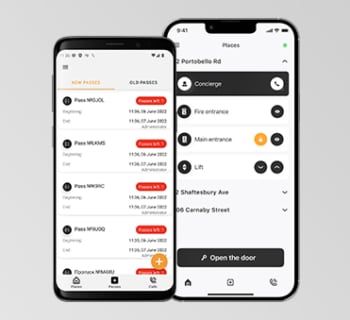
Ouvrir porte immeuble avec smartphone (iOS + Android)
Être loin, savoir que tout est en ordre chez vous, voir tous les invités et pouvoir répondre et ouvrir la porte, et être en contact avec le concierge 24h/24 et 7j/7. Notre application fait toutes les tâches. Tous les interphones immeuble BAS-IP ont la fonction ouverture de porte par défaut.

ACCÈS SANS CLÉ DEPUIS SMARTPHONE
Utilisez votre smartphone au lieu des porte-clés et des cartes d’accès pour entrer dans interphone multi-appartements. Aujourd’hui, lorsque vous devez entrer dans votre entrée ou votre complexe d’appartements, vous vous retrouvez inévitablement dans une situation où vous devez porter sur vous en permanence divers porte-clés et cartes d’accès. Il est assez facile de les perdre et ils ne sont pas toujours pratiques à utiliser. Vous pouvez utiliser un téléphone intelligent avec une application pour déverrouiller les portes avec BAS-IP. Vous pouvez également ouvrir des portes avec votre Apple Watch.

PASSES INVITÉS POUR VOITURES
La fonctionnalité vous permet d’intégrer des panneaux d’appel d’interphone collectif BAS-IP avec des caméras pour la reconnaissance du numéro et une ouverture supplémentaire de la barrière pour les voitures dont les numéros sont stockés dans la mémoire du système d’interphone. La fonction principale du système de reconnaissance des plaques d’immatriculation est d’automatiser le contrôle de l’accès des voitures aux zones protégées, d’éliminer l’influence du facteur humain, ainsi que d’organiser l’ouverture automatique de la barrière lorsque les voitures entrent / sortent du territoire.

BOUTON DE SORTIE SANS CONTACT
Bouton de sortie sans contact avec une durée de vie de plus de 100 millions de clics. Idéal pour les zones de passage avec un grand nombre d’entrées/sorties.

COMMANDE D’ASCENSEUR
Un résident du complexe peut ouvrir la porte à son invité à l’aide de l’interphone immeuble collectif, après quoi l’invité ne peut monter qu’à l’étage où habite le résident. Lors de l’ouverture de la porte d’entrée à l’aide de l’identifiant BAS-IP, l’ascenseur conduira le locataire directement à l’étage souhaité.

POSSIBILITÉ D’INSTALLER DES APPLICATIONS TIERCES
Les interphones multi-appartements BAS-IP disposent d’une interface graphique intuitive où le locataire peut télécharger ses photos ou des applications tierces.

INTÉGRATION À LA MAISON INTELLIGENTE
Le protocole SIP vous permet également de connecter l’interphone collectif au Smart Home et de recevoir des appels vers n’importe quel appareil client SIP. Notre équipement a été intégré avec succès avec des fabricants tels que KNX, Crestron et Control4. Vous pouvez également connecter des capteurs de mouvement au moniteur BAS-IP sur Android OS pour enregistrer la vidéo des caméras IP connectées lorsqu’un mouvement est détecté.
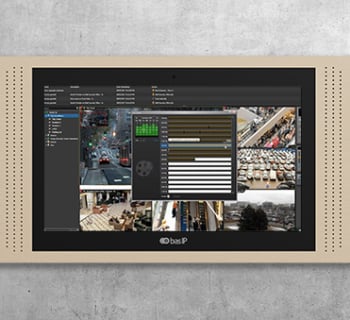
VISUALISATION DES CAMÉRAS DE SURVEILLANCE IP DEPUIS UN MONITEUR OU DEPUIS L’APPLICATION
Le locataire peut visualiser les caméras de surveillance installées sur le site sur son moniteur BAS-IP ou sur une application mobile. Il s’agit d’une fonction très recherchée dans un interphone collectif. Par exemple, les parents veulent garder un œil sur leur enfant dans la cour de récréation. Ou pour savoir si la voiture est en règle dans le parking.
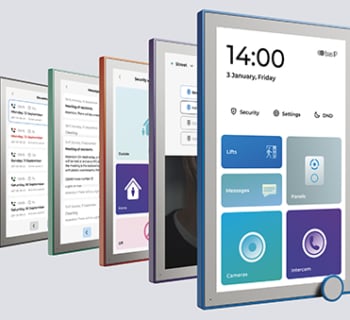
VARIÉTÉ DE DESIGNS ET DE COULEURS
Interphone immeuble collectif BAS-IP propose actuellement plus de 5 postes de porte différents, 7 moniteurs et des combinés audio pour répondre à tous les besoins des clients. Chaque modèle est également disponible en différentes couleurs, voire en différents matériaux.

CONTRÔLE D’ACCÈS INTÉGRÉ AVEC AUTHENTIFICATION MULTIFACTEUR
Pour le confort des résidents, nous offrons le maximum d’options pour accéder à l’objet – reconnaissance faciale, code pin, porte-clés, carte d’accès, NFC et Bluetooth. Et pas seulement pour eux, mais aussi pour leurs invités – nous proposons un accès invité par code QR, numéro de voiture ou clés virtuelles émises par les résidents. Pour une sécurité optimale, les résidents peuvent également combiner plusieurs types de contrôle d’accès en même temps.
Comparez l’interphone multi-appartements BAS-IP avec n’importe quel interphone collectif IP
Projets achevés
4 étapes pour commander le meilleur interphone immeuble collectif
Informations techniques pour la construction d’un système d’interphone collectif:

Schema de câblage d’un interphone immeuble à appartements
Pour votre commodité, nous vous aiderons à gérer le projet depuis le moment où vous contactez notre entreprise jusqu’à son installation finale. Nous voulons que vous sachiez que commander et installer notre interphone ne vous procurera que des émotions positives.
FAQ
Comment pouvons nous aider?
- Laissez-vous inspirer par notre produit Découvrez ce que nos équipements peuvent faire
- Devenez notre distributeur Développez votre activité avec BAS-IP
- Découvrez la partie technique Télécharger les instructions et les schémas de câblage
Nos contacts
- Département des ventes: sales@bas-ip.com
- Soutien technique: support@bas-ip.com